GRE数学考点之——概率
时间:2021-11-11 1020 16人参与

Tara老师
毕业于毕业于四川外国语大学,进修于美国威廉玛丽学院,拥有7年雅思口语/听力,托福口语科目教学经验,7年出国语言课程培训经验;雅思总分8分;剑桥大学英语教师资格证(CELTA)及TKT;英语专业八级;BEC商务英语高级学员出分率99.7%,学生好评分4.96分(满分5分)
概率是GRE数学中一个比较高频的考点,很多考生在面对这部分考题的时候觉得比较难,容易出错。造成考生们失分的原因之一就是对概率的概念掌握的不够清晰,没用到正确的方法和公式。今天我们就来为大家梳理一下概率相关的概念和公式,一起来看看吧~~
![src=]()
一、概念
概率:反应随机事件出现的可能性大小。
随机事件:指在相同条件下,可能出现也可能不出现的时间。事件A出现的概率记作P(A)。
若事件A必然发生,则P(A)=1;若事件A不可能发生,则P(A)=0。
所以,随机事件的概率介于0到1之间。
二、等可能事件
如果在一次实验中可能出现的结果总数为n个,并且所有结果出现的可能性都相同,那么每个基本事件互为等可能事件。如果事件A包含m个实验结果,那么事件A的概率:P(A)=m/n。
举例:
If four numbers are randomly selected without replacement from set {1, 2, 3, 4}, what is the probability that the four numbers are selected in ascending order?
A.1/256
B.1/64
C.1/48
D.1/24
E.1/12
解析:选4次4个数都要选,随机选择可能的总结果数是A(4,4)=24种。符合条件的选法数只有1种。设P(A)为“按照升序选出这4个数”的概率,则P(A)=1/24,所以答案选D。
三、互斥事件
若事件A和事件B不能同时发生,则称两个事件为互斥事件。
事件A和事件B同时发生的概率为:P(A∩B)=0
事件A或事件B有一个发生的概率为:P(A∪B)=P(A)+P(B)
The probability that event M will not occur is 0.8 and the probability that event R will not occur is 0.6. If events M and R cannot both occur, which of the following is the probability that either event M or event R will occur?
A. 1/5
B. 2/5
C. 3/5
D. 4/5
E.12/25
解析: 事件M和R不会同时发生,所以M和R是互斥事件。其中,M发生的概率P(M)=1-0.8=0.2,R发生的概率P(R)=1-0.6=0.4,所以事件M或者事件R发生的概率=P(M)+P(R)=0.2+0.4=0.6=3/5。答案选C。
四、相互独立事件
事件A不影响事件B的发生,则称两个事件为相互独立事件。
事件A和事件B同时发生的概率为:P(A∩B)=P(A)*P(B)
事件A或事件B有一个发生的概率为:P(A∪B)=P(A)+P(B)-P(A)*P(B)
In a probability experiment, G and H are independent events. The probability that G will occur is r, and the probability that H will occur is s, where both r and s are greater than 0.
Quantity A:
The probability that either G will occur or H will occur, but not both
Quantity B:
r+s-r×s
A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.
解析:G和H是独立事件,Quantity A 要求不包含同时发生的情况,也就是G发生H不发生概率和G不发生H发生的概率之和,即Quantiy A= r(1-s)+(1-r)s=r+s-2rs。因为r,s 不等于0 ,所以 r+s-2rs一定小与r+s-rs。答案选B.
Example 4:
A box contains 6 black balls and 4 white balls. If two balls are selected at random without replacement, what is the probability that both balls are white?
A.7/90
B.3/25
C.2/15
D.4/25
E.4/9
解析:balls总数是10个,不重复选取2个,取出第一个和取出第二个就是两个相互独立的事件。
设P(A)为“第一次取出的是white”的概率,P(B)=“第二次取出的也是white”概率,则P(A)=4/10=2/5,P(B)=3/9=1/3,P(AB)=P(A)P(B)=2/15,所以答案选C。
更多备考知识可点击下方,在线咨询哦~~
一、概念
概率:反应随机事件出现的可能性大小。
随机事件:指在相同条件下,可能出现也可能不出现的时间。事件A出现的概率记作P(A)。
若事件A必然发生,则P(A)=1;若事件A不可能发生,则P(A)=0。
所以,随机事件的概率介于0到1之间。
二、等可能事件
如果在一次实验中可能出现的结果总数为n个,并且所有结果出现的可能性都相同,那么每个基本事件互为等可能事件。如果事件A包含m个实验结果,那么事件A的概率:P(A)=m/n。
举例:
If four numbers are randomly selected without replacement from set {1, 2, 3, 4}, what is the probability that the four numbers are selected in ascending order?
A.1/256
B.1/64
C.1/48
D.1/24
E.1/12
解析:选4次4个数都要选,随机选择可能的总结果数是A(4,4)=24种。符合条件的选法数只有1种。设P(A)为“按照升序选出这4个数”的概率,则P(A)=1/24,所以答案选D。
三、互斥事件
若事件A和事件B不能同时发生,则称两个事件为互斥事件。
事件A和事件B同时发生的概率为:P(A∩B)=0
事件A或事件B有一个发生的概率为:P(A∪B)=P(A)+P(B)
The probability that event M will not occur is 0.8 and the probability that event R will not occur is 0.6. If events M and R cannot both occur, which of the following is the probability that either event M or event R will occur?
A. 1/5
B. 2/5
C. 3/5
D. 4/5
E.12/25
解析: 事件M和R不会同时发生,所以M和R是互斥事件。其中,M发生的概率P(M)=1-0.8=0.2,R发生的概率P(R)=1-0.6=0.4,所以事件M或者事件R发生的概率=P(M)+P(R)=0.2+0.4=0.6=3/5。答案选C。
四、相互独立事件
事件A不影响事件B的发生,则称两个事件为相互独立事件。
事件A和事件B同时发生的概率为:P(A∩B)=P(A)*P(B)
事件A或事件B有一个发生的概率为:P(A∪B)=P(A)+P(B)-P(A)*P(B)
In a probability experiment, G and H are independent events. The probability that G will occur is r, and the probability that H will occur is s, where both r and s are greater than 0.
Quantity A:
The probability that either G will occur or H will occur, but not both
Quantity B:
r+s-r×s
A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.
解析:G和H是独立事件,Quantity A 要求不包含同时发生的情况,也就是G发生H不发生概率和G不发生H发生的概率之和,即Quantiy A= r(1-s)+(1-r)s=r+s-2rs。因为r,s 不等于0 ,所以 r+s-2rs一定小与r+s-rs。答案选B.
Example 4:
A box contains 6 black balls and 4 white balls. If two balls are selected at random without replacement, what is the probability that both balls are white?
A.7/90
B.3/25
C.2/15
D.4/25
E.4/9
解析:balls总数是10个,不重复选取2个,取出第一个和取出第二个就是两个相互独立的事件。
设P(A)为“第一次取出的是white”的概率,P(B)=“第二次取出的也是white”概率,则P(A)=4/10=2/5,P(B)=3/9=1/3,P(AB)=P(A)P(B)=2/15,所以答案选C。
更多备考知识可点击下方,在线咨询哦~~
精选课程
热门推荐
- 1雅思口语话题——Describe a person who contributes to the society
 521人参与
7336121
521人参与
7336121
- 22021年全年托福高频写作题目汇总
 619人参与
335589
619人参与
335589
- 3如何进行有效的英文写作训练?
 152人参与
218092
152人参与
218092
- 4因疫情无法参加GMAT考试的考生,可免费退考或转考
 179人参与
2570104
179人参与
2570104
- 5去日本留学的条件:如何申请日本大学?
 821人参与
308251
821人参与
308251
阅读推荐
-
2022年3月、4月雅思考试取消通知(最新3月10日更新结果)
雅思2022-03-11

-
雅思考场红黑榜一览!
杭州雅思2023-04-25

-
托福写作改革:新题型和独立写作有什么不同?
托福2023-04-26
-
2023年4月26日最新托福考情来了!
杭州托福2023-04-27

-
IB数学AA和AI该如何选择才能拿7分?
英语学习2023-04-26

-
杭州GRE培训机构哪个好?
GRE2023-04-28

-
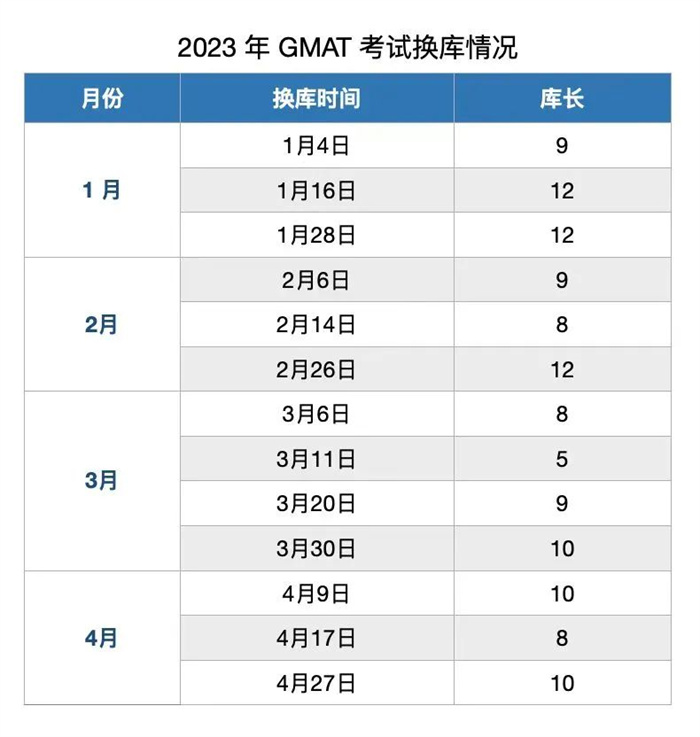
GMAT考试4月27日换库!机经解析+换库预测+考试安全期更新!
GMAT2023-04-27
-
杭州开设了AP课程的国际学校有哪些?
国际高中2022-03-03

-
普通高中在读转学A-Level课程,需要怎么做
出国留学2023-04-07

-
2023年AMC10如何备考?杭州有AMC10数学竞赛辅导机构吗?
其它原创2023-04-25









